I have a question about pool vector velocities

As the title above says, I have a question about pool vector velocities.

I am a computer programmer who spends part of his time each week teaching children programming and electronics. Recently we've been learning about various graphic systems and vector mathematics. I came up with the idea of writing a 2D pool table simulation to further demonstrate vectors. The simulation works well, but I think there is a problem and I am hoping someone reading this can help me.

I don't have a strong physics background, but I do have an understanding of the physics of the game of pool. Working backward from my understanding of pool physics I think have an acceptable simulation of pool physics useful for teaching, with the exception a problem dealing with velocities impact. I am unsure if I'm handling them correctly.

My simulation program

Here is a brief view of my simulation program. It's animated using my own step based physics solver and uses the small nanovg C library to render the visuals.

The variables

When the moving cue ball collides with stationary object ball the cue ball travels along vector at a velocity of . When it hits the object ball a line is drawn from the center of the cue ball to the center of the object ball creating vector . After the collision, the object ball changes velocity in the direction of vector . Finally the cue ball is deflected at a right angle of vector where it continues traveling in the direction of vector .

.

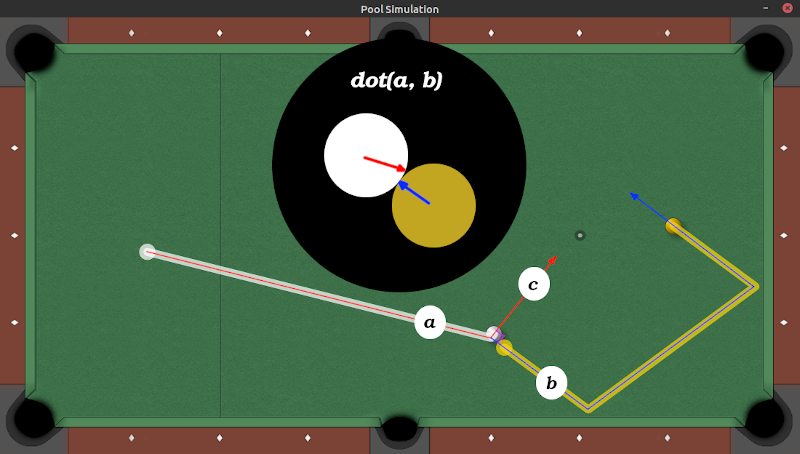
The problem

// vectors are normalized and only used for direction, not velocity
typedef struct {
  float x;
  float y;
} vec2;

// the vec2 dot product function
float dot(vec2 v0, vec2 v1) {
  return v0.x * v1.x + v0.y * v1.y;
}

// we have variables for direction vectors a, b, and c
vec2 a, b, c;
// and separate variables for their associated velocities av, bv, cv
float av, bv, cv;

// ...
// later in code assuming we already have
//   a, b, c already calculated
//   av already storing the incoming cue ball velocity

// i calculate the distribution of energy using dot(a, b)
float d = dot(a, b);
// and divvy up the energy of av into bv and cv using this logic
bv = av * d;
cv = av * (1 - d);

// but is this correct?

The problem is I'm unsure if I'm calculating the velocity of the outgoing object ball velocity and outgoing cue ball velocity correctly.

Here is what I'm doing to arrive at those two velocities. Perhaps some of you can tell me if this is correct.

I take the dot product of the vectors of the initial cue ball vector and the outgoing vector of the object ball.

Note: All direction vectors are normalized.

float d = dot(a, b);

Then I take the velocity of the cue ball and use it to create new velocities for and for the outgoing vectors of the object ball and cue ball respectively.

bv = av * d;
cv = av * (1 - d);

Essentially my thought is that the energy of the initial cue ball velocity is conserved (conservation of momentum) by splitting the velocity among the two outgoing vectors. I think the dot product between the two vectors and gives me which is the percent of velocity transferred to the object ball . While gives me remaining percentage of that velocity to transfer to the outgoing cue ball velocity .

Is this the correct way to handle splitting up the initial velocity of the cue ball?

I am asking because it doesn't seem right in my simulations. It seems that in most situations a disproportionate amount of energy is transferred to the object ball after a collision. As you can see in the image above, the cue ball travels very little after colliding with the object ball in this particular situation.

Finally, please understand I have simplified an explanation of my pool physics simulation for purpose of explaining the problem. I'm of course doing things like reducing ball velocities over time to simulate for friction and air resistance, and I am also reducing velocities a tiny amount when things collide to simulate energy loss. Also, this is a relatively simply 2D simulation, so ball spin / english is not taken into account.